QUÉ ES LA FRECUENCIA DE LAS NOTAS MUSICALES
¿De dónde surgen las frecuencias en la música? ¿Por qué suenan las notas musicales? ¿Tienen algo que ver con la existencia de octavas y semitonos? ¿Qué frecuencias puede percibir el oído humano?
Para entender qué es la FRECUENCIA DE LAS NOTAS MUSICALES lo primero que debemos tener claro es CÓMO SE PRODUCE EL SONIDO y qué es la FRECUENCIA DE VIBRACIÓN.
CÓMO SE PRODUCE EL SONIDO
El sonido se produce cuando un cuerpo vibra rápidamente. Este cuerpo al vibrar empuja a las partículas de aire que tiene más cerca, y éstas a sus vecinas, y éstas a sus vecinas... hasta que las últimas partículas de aire se introducen en nuestro oído a través del canal auditivo hasta el tímpano, al que también por empuje hacen vibrar. La vibración del tímpano estimula a su vez a los "huesecillos" que continúan transmitiendo ese movimiento vibratorio hasta las células nerviosas del oído interno, las cuales envían impulsos eléctricos hacia el cerebro en donde por fin son interpretadas como sonido.
A la propagación de una vibración a través de un medio elástico (como puede ser el aire) se la denomina "onda sonora".
 Como veis en este proceso de "empuje" lo que se va transmitiendo es una fuerza (una energía) que va afectando a todas las partículas de aire hasta que finalmente penetra en nuestro oído y se convierte en algo que podemos oír gracias a nuestro cerebro.
Como veis en este proceso de "empuje" lo que se va transmitiendo es una fuerza (una energía) que va afectando a todas las partículas de aire hasta que finalmente penetra en nuestro oído y se convierte en algo que podemos oír gracias a nuestro cerebro.Podemos concluir entonces con que no hay un transporte de materia desde ese objeto vibrante hasta nuestro oído. Las partículas de aire que están próximas a ese objeto no viajan hasta nuestro oído. Lo que va "viajando" es la fuerza que provoca esa vibración transmitiéndose de unas a otras.
Para sentir lo que es una vibración podéis "observar" vuestra lengua mientras hacéis "rrrrrrrrrrrrrrrrrr". ¿Notáis cómo vibra? Se mueve muy rápido. Podríamos decir que con cada "r" le damos un empujoncito a las partículas de aire cercanas a nuestra lengua. Con el empujón estas partículas chocan contra las siguientes, las cuales a su vez chocan contra las siguientes y así sucesivamente hasta que las últimas partículas estimulan nuestro oído.
Si el cuerpo que vibra lo hace muy despacio (r - - r - - r - - r - - r - - r - - r - - r) irá empujando a las partículas de aire vecinas de una forma más espaciada en el tiempo.
¿QUÉ ES LA FRECUENCIA DE VIBRACIÓN?
La frecuencia mide el número de repeticiones de cualquier fenómeno por unidad de tiempo. Se mide en hercios (Hz) que es la cantidad de veces que se repite ese fenómeno por segundo.
Por ejemplo, si yo digo que un fenómeno tiene una frecuencia de 2 hercios (2 Hz) significa que se repite 2 veces por segundo.
En el ejemplo de la vibración de nuestra lengua, si decimos que vibra a una frecuencia de 2 Hz, estaríamos diciendo que vibra 2 veces por segundo. (r - - r cada segundo)

La vibración de un cuerpo sonoro (como puede ser una cuerda de guitarra que pulsamos con un dedo) es un fenómeno repetitivo y por lo tanto podremos medir la frecuencia con que se produce su vibración. Vibrará cierto número de veces por segundo.
Como podéis observar en la imagen anterior de nuestra cuerda su frecuencia de vibración es más o menos de 1 Hz (1 Hercio), porque realiza una vibración completa cada segundo. Vibra muy despacio, tan despacio que incluso podemos ver el movimiento que realiza al vibrar. Su vibración es menor incluso de 1 Hz, pero para no liaros con decimales lo redondeo.
Cuando una cuerda vibra empuja a las partículas de aire que tiene más cerca, y éstas a las siguientes, y éstas a las siguientes... hasta que finalmente las últimas partículas estimulan nuestro oído. Y es entonces cuando oímos el sonido que produce.
Durante todo el tiempo que permanece vibrando una cuerda estará continuamente empujando partículas de aire.
Si la cuerda vibra muy despacio el sonido que producirá será MUY GRAVE, como la voz de un monstruo de voz ronca.
Si la cuerda vibra muy rápido el sonido que producirá será MUY AGUDO, como la voz de una fina señorita cuando chilla.
En el siguiente audio escucharéis:
- primero una cuerda de guitarra que vibra despacio, por lo tanto su sonido es grave.
- después una cuerda de guitarra que vibra deprisa, por lo tanto su sonido es agudo.
Contra más despacio vibre nuestra cuerda más grave será su sonido (pocos hercios Hz)
Contra más deprisa vibre nuestra cuerda más agudo será su sonido (muchos hercios Hz)
¿QUÉ FRECUENCIAS (O CANTIDAD DE VIBRACIONES POR SEGUNDO) PUEDE CAPTAR EL OÍDO HUMANO?
El oído humano no puede captar vibraciones demasiado lentas, ni vibraciones demasiado rápidas.
Es decir, que si una cuerda vibra muy pocas veces por segundo (pocos hercios) no oiremos ningún sonido, y si la cuerda vibra muchísimas veces por segundo (muchos hercios) tampoco oiremos nada.
Para que el oído humano pueda captar sonido la frecuencia de vibración de nuestra cuerda debe estar comprendida entre los 20 Hz y los 20.000 Hz. Es decir, que debe vibrar desde 20 veces por segundo hasta 20.000 veces por segundo.
La gama de frecuencias que va desde 20 a 20.000 Hz (que son las que podemos oír) forman lo que se llama "espectro Audible".
Las frecuencias menores de 20 Hz (las vibraciones MUY lentas) que no podemos oír constituyen los infrasonidos.
Las frecuencias mayores de 20.000 Hz (las vibraciones MUY rápidas) que no podemos oír constituyen los ultrasonidos.
LAS NOTAS MUSICALES SON VIBRACIONES
Como ya habréis adivinado las notas musicales también son sonidos producidos por vibración, la vibración de una cuerda al ser pulsada por nuestro dedo, por ejemplo.
Esa cuerda tendrá una tensión determinada y dependiendo de la tensión que tenga vibrará cierto número de veces por segundo al ser pulsada (x Hz). Y por lo tanto producirá un determinado sonido, o nota musical.
Cuando pulsamos una cuerda que está POCO TENSA vibra POCAS VECES por segundo (pocos Hz). Por lo tanto su sonido será GRAVE.
Aquí tenemos una nota DO GRAVE, ESCUCHAD:
Cuando pulsamos una cuerda que está MUY TENSA vibra MUCHAS VECES por segundo (muchos Hz). Por lo tanto su sonido será AGUDO.
Aquí tenemos una nota DO AGUDA, ESCUCHAD:
Lo que hacemos al AFINAR un instrumento de cuerdas, como puede ser una guitarra, es tensar cada una de sus cuerdas de manera tal que cada una vibre cierto número de veces por segundo y produzca el sonido que necesitamos.
Por ejemplo para conseguir el sonido de la nota LA tenemos que hacer que nuestra cuerda vibre 440 veces por segundo (440 Hz).
¿Por qué 440 Hz es la frecuencia de afinación del LA? Pues porque en 1955 la Organización Internacional de Estandarización así lo fijó. Se debe tener una nota de referencia para que todos los instrumentos puedan estar correctamente afinados y armonizados, y de esta manera puedan sonar en consonancia unos con otros. Y la nota de referencia elegida ésta vez fue el LA a 440 Hz.
Este valor de frecuencia de la nota LA ha ido variando a lo largo de los siglos según el gusto musical de las distintas épocas. Unas veces se llamaba LA al sonido producido por una vibración a 380 Hz, otras veces el LA era el sonido producido por una vibración a 422,5 Hz, otras a 480 Hz...
Como habréis adivinado los sonidos LA de 380 Hz y 422,5 Hz eran MÁS GRAVES que el sonido LA a 440 Hz que tenemos ahora, pues para producir aquellos LA las "cuerdas" vibraban menos veces por segundo.
Y el LA a 480 Hz era MÁS AGUDO que el de ahora a 440 Hz, pues la "cuerda" LA de aquella época vibraba más veces por segundo.
A partir de la nota de referencia (en nuestra época el LA a 440 Hz) se calcula el valor de la frecuencia de todas las demás notas mediante una operación matemática (que veremos al final de esta entrada). Y de ésta manera se consigue la misma afinación para todos los instrumentos musicales. En un momento veremos cuál es ésta operación.
¿Cómo cuento las veces que vibra mi cuerda para saber que tengo la nota LA afinada a 440 Hz? ¿Cómo sé que vibra 440 veces por segundo?
Obviamente no tenemos que contar nada. Sería de locos tratar de visualizar cuántas veces vibra nuestra cuerda (y el resto de cuerdas para las demás notas) . Para eso existen aparatos que "cuentan" esas vibraciones por nosotros. Se llaman AFINADORES, aunque también tenemos el DIAPASÓN. Analizaremos y aprenderemos a usar estos aparatos en una clase posterior.
NUESTRO SISTEMA MUSICAL TIENE 12 NOTAS
¿Pero no tenía 7 notas nada más: Do, Re, Mi, Fa, Sol, La y Si?
Pues no, tiene 12. Porque entre algunas de éstas notas existe un sonido intermedio que lleva el mismo nombre de las dos entre las que se encuentra, pero acompañado de una ALTERACIÓN (# o ♭). En un teclado podemos identificar estos sonidos intermedios con las teclas negras.
Fijaos en que una tecla negra tiene dos nombres, pues es el sonido intermedio que está entre dos notas. Puede tomar el nombre de la "nota/tecla" anterior a ella (en este caso llevará un #), o puede tomar el nombre de la "nota/tecla" posterior a ella (en este caso llevará un ♭).
Os pondré una imagen para que lo entendáis y debajo la explicaré.
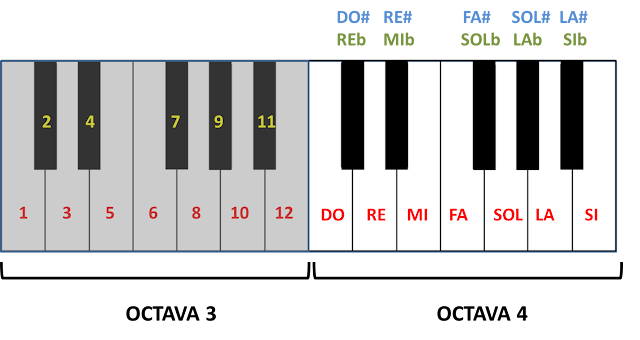
Observad cómo todos los nombres de teclas negras escritos en azul llevan un # (se han nombrado en base a la "nota/tecla" anterior). Y cómo los nombres de teclas negras escritos en verde llevan un ♭ (se han nombrado en base a la "nota/tecla" posterior).
No os preocupeis si ahora no entendéis el porqué de tener una misma tecla dos nombres distintos, lo explicaremos más adelante en otra clase. Pero os adelanto que el escoger un nombre u otro depende de la tonalidad en la que nos encontremos cuando interpretamos o componemos una obra musical.
INTRODUCCIÓN A LAS OCTAVAS
Un piano tiene alrededor de 88 teclas, unos algunas más y otros menos. Pero la mayoría de pianos modernos tienen 88 (52 blancas y 36 negras).
Todo el teclado está dividido en grupos de 12 teclas. Observad en la imagen anterior las teclas con números del 1 al 12, cuyos nombres he puesto en la parte derecha de la misma imagen.
El dibujo o diseño que veis en esas 12 teclas se repite 7 veces a lo largo de todo el teclado de nuestro piano de 88 teclas. Y nos "sobran" 3 teclas a la izquierda del todo y 1 tecla a la derecha del todo.
Observad la siguiente imagen:
Como veis cada grupo de 12 teclas se denomina OCTAVA.
Cada OCTAVA tiene los mismos nombres de notas que hemos visto anteriormente.
Pero escuchad cada una de ellas:
OCTAVA 1
OCTAVA 2
OCTAVA 3
OCTAVA 4
OCTAVA 5
OCTAVA 6
OCTAVA 7
Como podéis comprobar contra más pequeño es el número de la OCTAVA más grave es el sonido de sus 12 teclas. Y contra más grande es su número más agudo es su sonido.
Pero notamos que todas las octavas son similares. Cada OCTAVA es igualita a las demás, con la única diferencia de ser más grave o más aguda que el resto.
Si pulsamos todas las teclas de nuestro piano, de una en una, de izquierda a derecha, iremos desde la tecla más grave (a la izquierda del todo) hasta la tecla más aguda (a la derecha del todo).
Tras cada tecla de un piano se encuentra un mecanismo en el que un "martillo" golpea una cuerda (o varias).
Cuando pulsamos una tecla accionamos su martillo, que al golpear su cuerda le provoca una vibración. Esa cuerda se pone a vibrar, tal y como lo haría si la pulsáramos con un dedo.
Cada cuerda de cada tecla tiene una tensión determinada. Y como habréis adivinado, a medida que nos aproximamos a la derecha de nuestro teclado, las cuerdas van estando cada vez más tensas y por lo tanto van siendo más agudas. Comenzamos por la tecla de la izquierda del todo del teclado, que es la menos tensa y más grave, y terminamos con la tecla de la derecha del todo que es la más tensa de todas y la más aguda.
Recordad que contra menos tensa esté una cuerda más grave será su sonido, porque vibra pocas veces por segundo (pocos hercios). Y contra más tensa esté, más aguda sonará, porque vibra muchas veces por segundo (muchos hercios).
Podéis ver en éste video de "MitLab Tutorials" el mecanismo de un piano, y cómo cada tecla acciona un martillo que golpea su cuerda correspondiente:
La tecla más grave, a la izquierda del todo del teclado de nuestra imagen de colorines (que no tiene ningún color en ella) es un LA, y pertenecería a las teclas finales de la OCTAVA 0 (cero). Sería la tecla nº 10 de la imagen anterior que tiene los números de cada nota. Esa tecla pulsa con su martillo una cuerda que tiene una vibración de 27,5 hercios, es decir, que vibra 27,5 veces por segundo.
Escuchad el LA de la OCTAVA 0:
Es muy grave su sonido, y tiene muy poquitas vibraciones por segundo. Se acerca al límite inferior que puede captar el oído humano, que es de 20 hercios (mirad la imagen del "espectro audible" que puse antes).
Si hubiese algunas teclas más a la izquierda de éste primer LA, habría personas que no podrían oír nada (cada oído es distinto), y otras tal vez escucharían las más cercanas a éste LA. Por eso ya no se ponen más teclas hacia la izquierda. Aparte de que también su sonido sería tan grave que no se usaría para componer o tocar melodías, pues el sonido que producirían sería feo. De hecho las teclas más graves del piano no se utilizan casi nunca.
Lo mismo ocurre si observamos la tecla situada a la derecha del todo del teclado (también sin color en nuestra imagen del teclado de colorines). Esa tecla es la primera nota de la OCTAVA 8 (un DO). Corresponde a la tecla nº 1 en nuestra imagen con los números de cada nota. Y es la más aguda de todas (la que tiene su cuerda más tensa). La vibración de su cuerda cuando es pulsada por su martillo es de 4186,009 hercios, es decir que vibra 4186,009 veces cada segundo. Son muchísimas vibraciones por segundo, por eso suena tan agudo. A su derecha no hay ya más teclas, pero no porque no podamos oirlas, porque como podéis ver en la imagen del "espectro audible" el oído humano puede captar frecuencias de hasta 20.000 hercios. Sin embargo si hubiese más teclas serían tan agudas que su sonido sería bastante molesto.
Escuchad el Do de la OCTAVA 8:
RANGO DE FRECUENCIAS EN UN TECLADO DE 88 TECLAS
Así que tenemos que nuestro teclado de 88 teclas, desde su nota/tecla más grave hasta su nota/tecla más aguda recorre un rango de frecuencias que está comprendido entre: 27,5 hercios y 4186,009 hercios.
Empieza con la frecuencia más grave de 27,5 Hz y termina con la más aguda de 4186,009 Hz.
FÓRMULA PARA CALCULAR LAS FRECUENCIAS DE TODAS LAS NOTAS MUSICALES CONOCIENDO SÓLO UNA
1) LA FRECUENCIA DE CUALQUIER NOTA EN UNA OCTAVA ES EL DOBLE EN SU OCTAVA INMEDIATAMENTE SUPERIOR
Aunque ya explicaremos detalladamente en qué consiste una OCTAVA, os adelantaré, ya que estamos con el tema, que la FRECUENCIA de una nota/tecla cualquiera en una OCTAVA, es el doble en la OCTAVA siguiente.
Ejemplo:
En la siguiente imagen tenemos las OCTAVAS 3 y 4 de nuestro anterior teclado de colorines. He puesto las frecuencias que corresponden a cada nota:
Observad cómo las frecuencias de cada nota (las vibraciones por segundo) van aumentando paulatinamente a medida que nos dirigimos hacia la derecha del teclado. Las notas van siendo cada vez más agudas.
Ahora mirad cómo cada nota/tecla en la OCTAVA 4 tiene el doble de frecuencia que en la OCTAVA 3. Se han multiplicado por 2 las frecuencias de la OCTAVA 3, para lograr las de la OCTAVA 4.
Obviamente también sucede al revés, que si tenemos la frecuencia de una nota determinada en la OCTAVA 4, al dividirla entre 2 nos dará su frecuencia en la OCTAVA 3.
Ahora si quisiéramos las frecuencias de la OCTAVA 5 sólo tendríamos que coger las frecuencias de la OCTAVA 4 y multiplicarlas por 2.
Y si quisiéramos las frecuencias de la OCTAVA 2 cogeríamos las de la OCTAVA 3 y las dividiríamos entre 2.
Todas las notas DO de todas las octavas son DO, y suenan como DO. La única diferencia está en el número de vibraciones por segundo de sus "cuerdas", que hacen que sea una nota DO más grave o más aguda. Ésto es así para todas las notas, por supuesto.
Así que si tenemos las frecuencias de una OCTAVA completa, podremos calcular TODAS las frecuencias del resto de octavas existentes en nuestro teclado.
Podemos realizar la operación "a la cuenta la vieja" (como suele decirse), por ejemplo conociendo la frecuencia de nuestra nota DO de la OCTAVA 4 que tiene una frecuencia de 261,625565 Hz :
- Si queremos calcular la frecuencia de DO en la OCTAVA 7 "a la cuenta la vieja" podríamos hacer:
261,625565 Hz (octava 4) x 2 = 523,25113 Hz (octava 5)
523,25113 Hz (octava 5) x 2 = 1046,50226 Hz (octava 6)
1046,50226 Hz (octava 6) x 2 = 2093,00452 Hz (octava 7)
Pero esto es perder el tiempo (y más si tenemos que hacer lo mismo con todas las notas de una octava). Porque podemos simplificar nuestra operación matemática, mirad:
- hemos tenido que multiplicar nuestra frecuencia de DO inicial por 2, tres veces.
Hemos hecho:
Frecuencia de DO4 x 2 x 2 x 2 = Frecuencia de DO7 (los números junto a DO significan el número de la octava a la que nos referimos: Do1, DO2, DO3, DO4...).
Que es lo mismo que hacer:
Frecuencia de DO4 x 23= Frecuencia de DO7
Frecuencia de DO4 x 8 = Frecuencia de DO7
Fijaos en que hemos elevado el nº2 a 3 (23). Casualmente si restamos al 7 de OCTAVA 7, el 4 de OCTAVA 4, nos da ese 3 al que hemos elevado nuestro 2 (7 - 4 = 3).
Por lo tanto podemos llegar a la siguiente conclusión:
Nos encontramos en la OCTAVA 4 y conocemos las frecuencias de sus notas.
Si queremos calcular la frecuencia de cualquier nota en una octava superior a la que estemos, restaremos al número correspondiente a esa nueva octava (OCTAVA 7) el de la octava en la que nos encontremos (OCTAVA 4). 7 - 4 = 3.
Y nos dará el número (3) al que hemos de elevar 2 para multiplicarlo por la frecuencia inicial.
Entonces cogeremos una por una las frecuencias de las notas de nuestra octava 4, que ya conocemos, y las multiplicaremos una a una por 23. Así obtendremos todas las frecuencias de la octava 7.
Si queremos calcular la frecuencia de cualquier nota en una octava inferior a la que estemos, restaremos al número correspondiente a la octava en la que nos encontramos (OCTAVA 4) el de la nueva octava a la que queremos llegar (OCTAVA 2, por ejemplo). 4 - 2 = 2.
Y nos dará el número (2) al que hemos de elevar 2 para dividirlo entre la frecuencia inicial.
Entonces cogeremos una por una las frecuencias de las notas de nuestra octava 4, que ya conocemos, y las dividiremos una a una entre 22. Así obtendremos todas las frecuencias de la octava 2.
Si queremos calcular la frecuencia de cualquier nota en una octava superior a la que estemos, restaremos al número correspondiente a esa nueva octava (OCTAVA 7) el de la octava en la que nos encontremos (OCTAVA 4). 7 - 4 = 3.
Y nos dará el número (3) al que hemos de elevar 2 para multiplicarlo por la frecuencia inicial.
Entonces cogeremos una por una las frecuencias de las notas de nuestra octava 4, que ya conocemos, y las multiplicaremos una a una por 23. Así obtendremos todas las frecuencias de la octava 7.
Si queremos calcular la frecuencia de cualquier nota en una octava inferior a la que estemos, restaremos al número correspondiente a la octava en la que nos encontramos (OCTAVA 4) el de la nueva octava a la que queremos llegar (OCTAVA 2, por ejemplo). 4 - 2 = 2.
Y nos dará el número (2) al que hemos de elevar 2 para dividirlo entre la frecuencia inicial.
Entonces cogeremos una por una las frecuencias de las notas de nuestra octava 4, que ya conocemos, y las dividiremos una a una entre 22. Así obtendremos todas las frecuencias de la octava 2.
Recuerda que:
- dada una frecuencia en una octava determinada, será del doble en la octava inmediatamente superior.
- dada una frecuencia en una octava determinada, será de la mitad en la octava inmediatamente inferior.
Ten en cuenta ésto que acabamos de ver porque te servirá mucho a la hora de calcular frecuencias mediante la fórmula que veremos a continuación.
2) FÓRMULA PARA CALCULAR LA FRECUENCIA DE CUALQUIER NOTA CONOCIENDO SÓLO LA FRECUENCIA DEL LA4 (EL LA DE LA CUARTA OCTAVA) QUE ES DE 440 HZ
Como he dicho anteriormente la nota de referencia que tenemos en nuestro sistema musical occidental es actualmente el LA a 440 hz (porque la Organización Internacional de Estandarización así lo fijó en 1955). Y a partir de ésta nota de referencia se calculan las frecuencias que deben tener el resto de notas para que todos los instrumentos suenen correctamente afinados.
El LA a 440 hz está situado en la OCTAVA 4 (como podéis ver en la imagen anterior que tiene las frecuencias escritas en las teclas de un teclado).
Conociendo éste número 440 para el LA4, podemos calcular el resto de frecuencias de todas las notas y octavas. Aunque se podría conocer otra frecuencia cualquiera, no tiene porqué ser ésta de 440 del LA4, pero como 440 es una frecuencia que todo músico que se precie conoce, te recomiendo que tú también te la aprendas y realices las operaciones con ella.
2.1) TONO Y SEMITONO (INTRODUCCIÓN)
Antes de poner la fórmula hemos de introducir brevemente el concepto de SEMITONO, pues en ella se utiliza.
Un SEMITONO es la mínima distancia (en vibraciones por segundo) que hay entre dos notas (en el sistema musical occidental nuestro, ya que por ejemplo en el sistema musical árabe tienen también cuartos de tono). Explicaremos el origen del semitono en nuestra siguiente clase y entenderéis perfectamente de dónde viene ese concepto.
Os volveré a poner una imagen anterior, para que la tengáis más cerca:
¿Cuál es la distancia mínima que observamos en este teclado entre dos notas?
Pues obviamente la mínima distancia la podemos encontrar entre una tecla y la siguiente 😉.
O lo que es lo mismo, entre una nota y la siguiente.
Entonces entre cualquier tecla de un teclado y la siguiente (sean blancas o negras) habrá un SEMITONO de distancia.
Habrá un SEMITONO de distancia entre las teclas:
1 y 2 - Do y Do# (o Re♭)
2 y 3 - Do# (o Re♭) y Re
3 y 4 - Re y Re# (o Mi♭)
4 y 5 - Re# (o Mi♭) y Mi
5 y 6 - Mi y Fa
.... etc
Obviamente también habrá un SEMITONO de distancia entre una tecla y la anterior 😊.
En una guitarra habrá un semitono entre un traste y el siguiente (o el anterior). Explico las cosas con teclado porque es mucho más fácil de entender.
La cuestión está en que tenemos 12 notas (o 12 teclas) en una OCTAVA cualquiera. Pero alguien en su momento tuvo que realizar una operación matemática gracias a la cual pudo dividir esa OCTAVA en esas 12 partes. Y al hacer esa operación le salió la distancia (en frecuencias) que debe separar a una nota de la siguiente para que le entrasen las 12 en el rango de una octava. Y esa distancia de separación entre dos notas es lo que llamamos SEMITONO. Como las notas musicales son vibraciones que producen un determinado sonido, pues obviamente esa distancia no es en metros, sino en vibraciones.
Ésto debió preguntarse nuestro matemático: ¿Cuántas vibraciones deben separar a una nota de la siguiente para que me entren en una OCTAVA las 12 que quiero poner para la música en occidente?
Tened en cuenta que ésta separación entre notas a la que llamamos SEMITONO no es siempre la misma. Es decir, no esperéis encontraros una cantidad siempre fija de frecuencias entre nota y nota.
Ésto ocurre porque con las frecuencias los cálculos llevan una progresión distinta, que ya explicaremos en nuestra siguiente clase, en la que veremos de dónde sale el SEMITONO.
Tampoco os hace falta calcular nada para ser músicos. Simplemente el propósito de toda esta clase es que podáis entender levemente lo que son las frecuencias, así como lo que son los semitonos, las octavas..., para que sepáis de dónde viene la música y el por qué de muchas cuestiones que iréis viendo respecto a ella.
En relación al semitono, simplemente debéis saber que "hay un SEMITONO entre cualquier nota y la que tiene al lado, sea la anterior o la posterior".
Ésto lo debéis tener muy claro porque vais a utilizarlo mucho.
Ahora veremos lo que es un TONO, que también lo usaréis tanto como el SEMITONO:
Analicemos la palabra SEMITONO:
SEMI: es un prefijo que significa "medio" o "casi". Y luego tenemos la palabra TONO (que por ahora no sabemos qué significa).
Nuestra palabra SEMITONO se transforma ahora en la expresión: "MEDIO-TONO" o "CASI-TONO".
Si un SEMI-TONO es la mitad de un TONO... ¿Qué necesitaremos para formar un TONO? 😖
¡Exacto! Dos SEMITONOS.
Un TONO estará formado por dos SEMITONOS consecutivos (vecinos).
Un TONO por lo tanto es la distancia que abarcan dos SEMITONOS.
Mira la siguiente imagen:
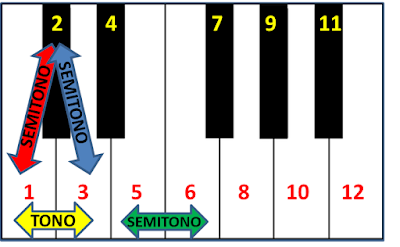
Entre las notas 1 y 2 hay un semitono de distancia (flecha roja).
Entre las notas 2 y 3 hay un semitono de distancia (flecha azul).
Podemos concluir entonces que entre las notas 1 y 3 habrá un TONO de distancia (flecha amarilla).
También hay un SEMITONO de distancia entre las teclas 5 y 6 (flecha verde).
Y otro semitono entre las notas 6 y 7 (aquí no puse ya más flechas)
Por lo tanto entre las notas 5 y 7 habrá también un TONO de distancia.
Ejercicio:
¿Cuantos SEMITONOS de distancia habrá entre la nota Do y la nota Sol (o lo que es lo mismo entre las teclas 1 y 8 de la anterior imagen)?
Haremos lo siguiente:
Entre las teclas 1 y 2 hay un semitono.
Entre las teclas 2 y 3 hay un semitono.
Entre las teclas 3 y 4 hay un semitono.
Entre las teclas 4 y 5 hay un semitono.
Entre las teclas 5 y 6 hay un semitono.
Entre las teclas 6 y 7 hay un semitono.
Entre las teclas 7 y 8 hay un semitono.
Total de semitonos: 7
Respuesta: hay un total de 7 semitonos entre las teclas 1 y 8 (entre Do y Sol).
Pero no hace falta hacer todo lo anterior.
Simplemente contaremos con los dedos a partir de la primera nota que nos den, en este caso a partir de la tecla 1 (o DO), hasta llegar a la última que nos den, en este caso la tecla 8 (o SOL).
Fijaos (recordad que es A PARTIR DE LA PRIMERA NOTA), id subiendo dedos para contar las teclas:
2, 3, 4, 5, 6, 7 y 8 (no hemos contado la tecla 1).
O lo correcto sería: Do#, re, re#, mi, fa, fa# y Sol (no hemos contado la nota Do).
Si contáis vuestros dedos tendréis levantados 7.
Es MUY IMPORTANTE saber contar semitonos (y tonos). Nos hará mucha falta a lo largo de toda la música.
¿Cuántos TONOS habrá entonces entre las mismas teclas 1 y 8 (entre Do y Sol)?
Si un TONO está formado por dos SEMITONOS, y aquí tenemos 7 semitonos, entonces sólo tenemos que dividir 7 entre 2. Y nos saldrá 3,5 TONOS. Es decir, que entre Do y Sol habrá tres tonos y medio.
2.2) Y POR FIN LA FÓRMULA DEL CÁLCULO DE FRECUENCIAS
Si necesitáis una calculadora en la que se puedan calcular raíces cuadradas y potencias, os dejo el siguiente enlace:
https://web2.0calc.es/
Como ya dije antes, con conocer una frecuencia cualquiera (como por ejemplo, y por ser la más fácil de recordar, la del LA a 440 hz, que es el LA de la OCTAVA 4), podemos calcular cualquier frecuencia con una fórmula y ayudados por los conocimientos que hemos aprendido en esta inmensa entrada de nuestro blog 😃.
Aquí va la fórmula:
No os asustéis al ver la fórmula, ya veréis que es más sencilla de lo que parece, y pondremos ejemplos después de explicarla un poco.
Como véis hay que multiplicar la frecuencia CONOCIDA (que en nuestro caso es 440 hz del LA4) por la raíz doceava de 2 elevada al número de SEMITONOS que separan la nota CONOCIDA de la que queremos calcular.
En caso de querer calcular una frecuencia más aguda que la conocida, la raíz doceava de 2 se eleva al número de semitonos de separación entre ambas notas (el LA4 y la que queremos calcular).
Y en el caso de querer calcular una frecuencia más grave que la conocida, ésta raíz se eleva al número de semitonos de separación entre ambas notas, pero con signo negativo, como ves en la imagen anterior.
La raíz doceava de 2 es 1,0594630943592953 (os la he puesto con todos los decimales). Por lo que podemos sustituir dicha raíz por éste largo número, y así nos quedaría algo más "sencillo":
440 x 1,0594630943592953semitonos de separación (ó -semitonos de separación)
El utilizar la raíz doceava de 2 en ésta fórmula lo veremos en nuestra siguiente entrada en la que hablaremos ya más a fondo de los SEMITONOS. Y entonces comprenderéis porqué se utiliza dicha raíz.
Vamos con algunos ejemplos, para ello os voy a poner de nuevo la imagen de un teclado que tenía puestas en varias teclas las frecuencias:
Calculando la frecuencia de una nota MÁS AGUDA que nuestro La4:
Conozco la frecuencia del La4 que es 440 hz. Y quiero calcular la frecuencia de la nota Si4 (el Si de la cuarta octava). Ésta nota Si4, como véis, está situada a la derecha del La4, por lo tanto es más aguda, y por lo tanto los "semitonos de separación" NO van a llevar signo negativo en nuestra fórmula.
Lo primero es ver cuántos semitonos separan ambas notas, y para ello contamos las notas A PARTIR de la primera (que es el La4), como os expliqué anteriormente. Nos disponemos a contar con los dedos (o mentalmente 😎):
La#, Si. (no hemos contado el La4, porque es A PARTIR de ella lo que debemos contar).
Vemos que hay 2 semitonos de separación.
Por lo tanto el número al que hemos de elevar la "raíz doceava de 2" es a 2.
Sustituímos la "raíz doceava de 2" por su valor: 1,0594630943592953, y nuestra fórmula nos quedará:
440 x 1,05946309435929532 = Frecuencia de Si4
440 x 1,12246204830937305652440951260209 = 493,8833012561241448707401855449196
Podéis comprobar en la imagen anterior que la frecuencia de la nota Si4 es exactamente la que nos ha salido en la fórmula. Os he puesto todos los decimales y tal vez no hiciese falta, pero así nuestros cálculos son más correctos.
Calculando la frecuencia de una nota MÁS GRAVE que nuestro La4:
Conozco la frecuencia del La4 que es 440 hz. Y quiero calcular la frecuencia de la nota Mi4 (el Mi de la cuarta octava). Ésta nota Mi4, como véis, está situada a la izquierda del La4, por lo tanto es más grave, y por lo tanto los "semitonos de separación" SI van a llevar signo negativo en nuestra fórmula.
Lo primero es ver cuántos semitonos separan ambas notas, y para ello contamos las notas A PARTIR de la primera (que es el La4), como os expliqué anteriormente. Nos disponemos a contar con los dedos (o mentalmente), ésta vez hacia abajo del teclado (es decir hacia la izquierda):
Sol#, Sol, Fa#, Fa, Mi. (no hemos contado el La4, porque es A PARTIR de ella lo que debemos contar).
Vemos que hay 5 semitonos de separación.
Por lo tanto el número al que hemos de elevar la "raíz doceava de 2" es a -5 (observad el signo negativo).
Sustituímos la "raíz doceava de 2" por su valor: 1,0594630943592953, y nuestra fórmula nos quedará:
440 x 1,0594630943592953-5 = Frecuencia de Mi4
440 x 0.7491535384383406241 = 329,627556912869874604
Podéis comprobar en la imagen anterior que la frecuencia de la nota Mi4 es exactamente la que nos ha salido en la fórmula.
¿QUÉ OCURRE SI LA FRECUENCIA QUE QUEREMOS CALCULAR ESTÁ EN OTRA OCTAVA, Y ES UNA NOTA MUY ALEJADA DEL LA4 A 440 HZ?
Podemos utilizar ahora lo de que: LA FRECUENCIA DE CUALQUIER NOTA EN UNA OCTAVA ES EL DOBLE EN SU OCTAVA INMEDIATAMENTE SUPERIOR, que vimos anteriormente, para hacer nuestros cálculos más sencillos.
Si no utilizamos este "truco" tendremos que contar un montón de semitonos que serán los que separen nuestro La4 de esa nota tan alejada de ella, de la cual queremos calcular la frecuencia.
Por ejemplo, queremos calcular la frecuencia del Do3 (fijaos lo separada que está del La4, en la imagen anterior).
Do3 está a la izquierda del La4, por lo tanto es una nota más grave, y por ello los "semitonos de separación" van a llevar signo negativo en nuestra fórmula.
Podemos ponernos a contar con los dedos los semitonos desde La4 hasta Do3. Recordad que empezamos a contar A PARTIR del La4, y que vamos hacia abajo del teclado (hacia la izquierda):
Sol#4, Sol4, Fa#4, Fa4, Mi4, Re#4, Re4, Do#4, Do4, Si3, La#3, La3, Sol#3, Sol3, Fa#3, Fa3, Mi3, Re#3, Re3, Do#3, Do3
Tenemos 21 semitonos de separación, y nos hemos pasado un buen rato contando notas con los dedos.
Ahora aplicaríamos la fórmula:
440 x 1,0594630943592953-21 = Frecuencia de Do3
440 x 0.297301778750680057844843 = 130.81278265029922545173092 sería la frecuencia de nuestro Do3. Podéis comprobarlo en la imagen anterior del teclado con las frecuencias escritas en él.
Pero podríamos simplificar un poco éstos cálculos si en lugar de contar todos los semitonos hasta Do3, los contásemos hasta Do4 (por eso os he subrayado el Do4 en los 21 semitonos que hemos contado y escrito aquí arriba).
Es decir, que en lugar de calcular la frecuencia de Do3, calcularemos la de Do4, que está más cerca del La4. Y una vez conocida la frecuencia de Do4, si la dividimos entre dos obtendremos ya directamente la frecuencia de Do3.
Vamos a hacerlo:
Lo primero, como siempre ¿cuántos semitonos de separación hay entre La4 y Do4?
Sol#4, Sol4, Fa#4, Fa4, Mi4, Re#4, Re4, Do#4, Do4
Hay 9 semitonos de separación entre La4 y Do4.
En la fórmula del cálculo de frecuencias estos semitonos llevarán un signo negativo (porque vamos hacia la izquierda del teclado, ya que queremos calcular una frecuencia más GRAVE)
440 x 1,0594630943592953-9 = Frecuencia de Do4
440 x 0.5946035575013603544 = 261.625565300598555936 (sería la frecuencia de Do4).
Ahora, como sabemos que la frecuencia de una nota en una octava es el doble en su octava inmediatamente superior, también podemos deducir que será la mitad en su octava inmediatamente anterior.
Tenemos la frecuencia de Do4 y queremos calcular la de Do3, que está en una octava INFERIOR, por lo tanto dividiremos la frecuencia de Do4 entre 2.
261.625565300598555936 (Frec de Do4) / 2 = 130.812782650299277968 (que es la frecuencia de Do3). Podéis comprobar estas frecuencias en la imagen del teclado anterior.
Vemos un ligero error de los decimales finales en el resultado de la frecuencia de Do3 que nos ha salido ahora, respecto a la que nos salió contando los 21 semitonos. Ésto seguramente será debido a que realizamos los cálculos con todos los decimales, y posiblemente sea un error de calculadora.
Bueno, por fin hemos llegado al final de nuestra inmensa clase de hoy. Espero que os hayan quedado claros todos los conceptos vistos en ella. Si no es así ya sabéis, podéis preguntar lo que creáis conveniente en los comentarios, y estaré encantada de responder.
¡Hasta la próxima clase!









Se me ha hecho un poco denso, hay que trabajar en la nasa para entender las fórmulas, por qué iría por letras. Seguro que los de ciencias lo leen y se ríen.
ResponderEliminarJajajajajaja no entiendo muy bien tu comentario pero creo que lo de trabajar en la nasa era ironía jajaja
EliminarExcelente explicación . Por lo menos a mí me gusta ir al meollo del asunto cuando aprendo algo. No aprender si porque si
EliminarExcelente trabajo, Gracias...!
ResponderEliminarExplicación cojonuda. Muchas gracias :)
ResponderEliminarUna sola palabra: Excelente!!
ResponderEliminarMuchas gracias, me alegro que no os hayáis desmayado por la extensión de ésta entrada, jajaaaaaaaaaa. Gracias por leerla.
ResponderEliminarMuchas gracias!!! soy de aquellos que gustan tomarse tiempo en leer para entender las cosas a profundidad y tu entrada me ha gustado muchísimo!!!! MIL GRACIAS!! Un abrazo desde Lima, Perú
ResponderEliminarExcelente explicación, muy bueno
ResponderEliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarEstá excelente tu trabajo pero hay un punto en el que creo no concordar con lo que has expuesto y es acerca del número de notas que mencionas que tiene una octava y es que precisamente el nombre de octava viene porque esta conformado por un intervalo de ocho notas naturales y se caracteriza por tener la misma nota en el inicio y en el final a diferente frecuencia de sonido por supuesto y es en ese intervalo de ocho notas naturales que en total suman 13 notas junto con las 5 alteraciones que vienen a ser los sostenidos o bemoles, y no siendo como tu indicas que en las octavas existen 12 notas. Quisiera saber tu opinión y si confirmas lo que yo digo o tal vez me tengas que aclarar lo contrario pero a mi parecer yo estoy en lo correcto en que en una octava hay 13 notas y no 12.
ResponderEliminarHola, disculpa la tardanza.
EliminarPuedes leer ésta entrada sobre las OCTAVAS a ver si te aclara algo.
https://www.ciudadpentagrama.com/2018/08/octava-musical.html
Te había hecho una respuesta tan grande que no me la admite Blogger por tener montones de caracteres, jejeee. Lee ese enlace y si sigues dudando pregunta.
Por aclararte algo: mira la última imagen que puse aquí (no en el enlace) que es de un teclado amarillo y verde con 2 octavas. Fíjate en el Do de color verde. Si perteneciera a la octava de color amarillo (según tú) y además perteneciera a la de color verde, resulta que ese Do pertenecería a la vez a 2 octavas y eso no puede ser. O pertenece a la octava 3, o a la 4.
Me quedo con la sensación de no aclararte nada, pero lee ese enlace y luego me dices si te quedó más claro.
Excelente, de todas las vces que lei o me explicaron sobre el tema es la primera vez que siento que lo voy entendiendo, gracias!!!!
ResponderEliminarSeguro que nadie se había enrollado antes tanto como yo, jajaaaa, gracias por aguantar el rollo.
EliminarbUENOS DÍAS... RECIEN ME ENTERO DE ESTE SITE Y ME PARECE MUY DIDACTICO... ES POSIBLE PODER VER LAS CLASES DESDE EL PRINCIPIO
ResponderEliminarBuenas tardes vine aquí porque no sabía mucho del tema pero estoy en la música y toco la guitarra así que debía leer esto casi por deber, la verdad me sorprendió la forma en que te extendías en los párrafos para que el lector se retroalimentará y contuviera las ideas presentadas ya que repetías de nuevo jajajaja eso es enseñar bien por otra parte entendí todo claramente por lo mismo y pensé que las fórmulas sería súper difíciles y no lo eran, espero poder seguir leyendo artículos como este, Mil gracias lo explicaste de forma muy sencilla.
ResponderEliminarGracias, me enrollo como una persiana, jajaaaa, pero es para que quien no sepa mucho se pueda enterar, aunque tal vez con tanto rollo consiga lo contrario, jejeeeeeeeeeeeeeeeeeee
Eliminar